

The result is frequencies that are equally spread out along the x-axis. For instance, when you make an FFT graph, each centimeter along the x-axis might represent a certain amount of frequency (100 Hz, say).
Music note c in hertx how to#
When you make a graph, you choose how to space the numbers along the axis. The bottom line is that humans perceive musical pitch in terms of the logarithm of frequency- rather than the frequency itself. Now, moving one key along the keyboard always increases the common log of frequency by the same amount- about 0.025. If you plot the logarithms of the frequencies above each of the notes instead of the actual frequencies, the picture of the piano becomes linear: Logarithms of frequencies of notes on the piano. If your understanding of math is really good, you probably notice that the math for the piano is identical to the math for compound interest at 6%! That’s because the relationship between pitch perception and frequency is logarithmic. Put another way, the frequency ratio between one piano key and the next is about 1.06. What remains the same is the percent increase– as you move one key to the right, the new frequency is about 6 percent higher than the previous note. At the top end of the piano, moving over one key increases the frequency by over 200 Hz. On the lowest note of the piano, moving one key to the right increases the frequency by less than 2 Hz. As you move one piano key to the right, the frequency does not increase by a specific number of Hertz. That’s because musical intervals are based on multiplication- not addition. What might be surprising is that the graph is not a line. That’s not surprising- higher pitched notes are at the right end of the piano. The bars get taller as you go to the right. The diagram below shows the frequencies of every note on the piano keyboard. Which is a larger musical interval: from 1000 Hz to 2000 Hz, or from 2000 Hz to 3000 Hz?.What is the musical interval between the notes? One note is 200 Hz higher than another note.What is the frequency of the note two octaves above a note with a frequency of 300 Hz?.Frequency differences tell you almost nothing about perceived pitch differences. Two frequencies that are a factor of two apart always sound an octave apart, no matter whether the two frequencies are 500 Hz and 1000 Hz or 10,000 Hz note and 20,000 Hz. The octave reveals something important about music and pitch perception: human perception of the “distance between two pitches” depends on the frequency ratio of the two notes- the bigger the ratio, the further apart the pitches seem. The note an octave lower (A3) has a fundamental of 220 Hz. The note an octave higher (A5) has a fundamental of 880 Hz. The note to which orchestras tune (A4) has a fundamental of 440 Hz- sometimes called A440. Second, an octave corresponds to a factor of two in frequency. First, an octave is especially easy on the ears- two notes an octave apart can be difficult to tell apart, especially when played together. The octave is a really important interval for two reasons. You’ve probably heard an octave before- both “Somewhere over the Rainbow” and “Chestnuts Roasting on an Open Fire” start with an octave jump. The interval from one A to the next A (or one D to the next D) is called an octave. The octaveĭistances along the piano keyboard are called musical intervals- intervals, for short.

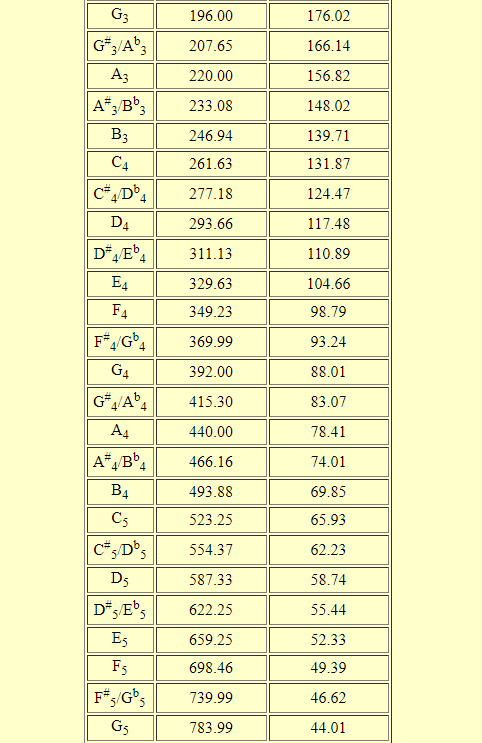
To hear how the piano keyboard is organized, play around with this five octave online keyboard or this small Flash keyboard with labeled keys. Note names on part of the piano keyboard. The diagram of a small section of the piano keyboard below illustrates the idea. To distinguish between different A’s, the lowest A on the piano is labeled A0, the next lowest A is labeled A1 and so on. The piano’s white keys are labeled A through G. Not surprisingly, musical notes are labeled using a cycle. On the piano, keys are arranged in order of pitch, with the lowest frequencies at the far left of the keyboard. Look at the keyboard carefully, and you’ll notice a repeating pattern of twelve keys. Perception of sound 12 Frequency ratios and pitch perception Piano keyboard


 0 kommentar(er)
0 kommentar(er)
